 Решение задач по теме "Системы счисления"
Решение задач по теме "Системы счисления"1)Основание системы счисления - количество цифр, которые используются в системе счисления. Например, в десятичной системе счисление основание равно 10.
Примеры алфавитов нескольких систем
Двоичная: 0 1
Восьмеричная 0 1 2 3 4 5 6 7
Шестнадцатеричная:
0 1 2 3 4 5 6 7
8
1. Последовательно выполнять деление данного числа на основание новой системы счисления до тех пор, пока получим неполное частное, меньшее делителя;
2. Составить число в новой системе счисления, записывая остатки в обратном порядке, начиная с последнего частного.
Пример 1: Перевести число 37 из десятичной в двоичную систему счисления.
Будем делить 37 на 2, записывая в первый столбик частное, во второй остатки при делении.
| 37 | 1 | ||
| 18 | 0 | ||
| 9 | 1 | ||
| 4 | 0 | ||
| 2 | 0 | ||
| 1 |
Ответ: 3710=1001012
3) Алгоритм перевода чисел из различных систем счисления в десятичную.
Вспомним как мы раскладывали число по разрядам по математике в пятом классе.
8903=8 * 1 000 + 9 *100 + 0 *10 +3 =8 *103 + 9 * 102 +0 * 101 +3*100
44,54=4*101+4*100+4*10-1+4*10-2
Чтобы перевести число из какой – нибудь системы счисления в десятичную нужно разложить его по разрядам и выполнить вычисления.
| разряды 3 | 2 | 1 | 0 |
| 8 | 9 | 0 | 3 |
ПРИМЕР 1: Перевести число из двоичной системы счисления в десятичную
10110002=1*26+0*25+1*24+1*23+0*22+0*21+0*20==8810
Пример 2. Перевести число из шестнадцатеричной в десятичную.
15FC16=1*163+5*162+15*161+12*160=562810
ПРИМЕР 4 0,1235=1*5-1+2*5-2+3*5-3=0.30410
4) Основные операции в двоичной системе счисления
СЛОЖЕНИЕ 0+0=0 0+1=1 1+0=1 1+1=10

ВЫЧИТАНИЕ 0-0=0 1-1=0 1-0=1 0-1=1 (заем из старшего разряда)

УМНОЖЕНИЕ 1*1=1 1*0=0 0*1=1 1*1=1
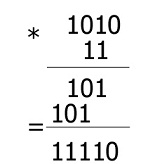
ДЕЛЕНИЕ 1:1=1 0:1=0
1010|10
10 101
10
10
0
Перевод чисел из двоичной в восьмеричную, шестнадцатеричную и обратно